Back Tapered shafts and why they are so effective!
Credit: Paul Fender from Fender Archery
Having nothing better to do, one day, I wanted to look at the vibrations that are created in an arrow upon release. I knew that I couldn’t really test or view what happens to an arrow during its entire flight. I realized though that I could test a bench top “simulation.” Using a digital storage oscilloscope (DSO), and an RPM sensor out of an old automotive electronic ignition, I was able to precisely time how long different arrows vibrated when I plucked on them and set them to vibrating. I knew the sensor would be sensitive to the steel of the arrow’s point.
A side note here. I realize that my little test is not real life. But I believe that it is reasonable to figure that the arrow’s behavior on the test bench would at least mimic real life and give us a good clue as to what is going on.
The pic “The Test Rig” shows my whole set up.

“Sensor” is the sensor I salvaged out of an old Honda distributor.

“Oscilloscope” is my Snap-On DSO. (I tell you this thing is way cool.)

And “Fixed Point” just shows that I simply clamped down one end of the test arrows.

Fixed Point
After an evening of sorting through my woodies I was able to find two arrows that had the same static spine and same weight (within 10 grains) one parallel, one tapered. Both had the same point weight. I made sure to clamp each arrow so that they both had equal free lengths and same distance from the sensor. Making sure to pull each arrow down the same distance each time, all I had to do was release it and I was able to “see” the vibrations on the DSO and time them. I did this 10 times for each arrow and took an average.
“Parallel” is a snapshot taken from the test run with the parallel shaft and is an example of what the DSO was showing me.
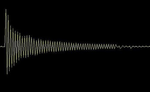
Parallel
Well folks, sure enough, there is a difference! The parallel shafts vibrated an average of .75 second LONGER than the tapered shafts! That was encouraging, so just for the heck of it I tested a few more different arrows but without bothering to match weight and spine. Naturally there started to be some overlap on some of the arrow’s results. However even without controlling for spine or total weight, as long as the arrows were correctly positioned and had the same point weight, it got even better with the tapered shafts vibrating for 1.25 second less time on average.
Not wanting to go too far off the reservation though, here are the average vibration times from the “controlled” shafts.
Tapered – 6.1 seconds
Parallel – 6.8 seconds
“Tapered Harmonics” is a sample of what I was seeing when testing the tapered shafts. This is where it gets interesting, so I highlighted the waveform in red. Notice how the amplitude, the signal strength, gets weaker and then stronger in ever diminishing waves until the vibrations are damped out. I believe that this is an important clue as to WHY tapered shafts recover from paradox faster.
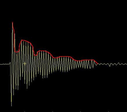
Tapered Harmonics
One time …..at band camp….I learned that things can vibrate at resonant frequencies. A so called “standing wave” is created. The pic “Standing Wave” is an illustration of a cylinder resonating at different standing wave resonant frequencies.
Tapered Harmonics
One time …..at band camp….I learned that things can vibrate at resonant frequencies. A so called “standing wave” is created. The pic “Standing Wave” is an illustration of a cylinder resonating at different standing wave resonant frequencies.
Standing Wave
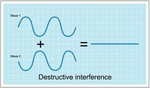
Standing waves tend to be self reinforcing and can persist for very long periods of time even without putting more energy into whatever is vibrating. I have a hypothesis, (which I doubt I could ever prove) that the unique vibration of a tapered shaft is caused by what is called “destructive interference.” The pic “Destructive Interference” illustrates the idea.
Destructive interference
The arrow attempts to fall into a resonant frequency, but as the vibrations travel up and down the shaft, when they hit the beginning of the taper some of the vibration energy is reflected back against the incoming wave. Not only does the effect get greater and greater due to the taper, but the taper also helps make the reflection more and more out of phase with the incoming vibrations. The reflections are chaotic and create destructive interference. The transition from regular cylinder to tapered cone helps to actively damp out standing wave vibrations.
So although tapered shafts DO recover from paradox faster than parallel shafts, there is what I would call the “Time Problem.” Although the addition of fletching must have an affect on paradox recovery, if an arrow is leaving a bow at say 180 fps, can an arrow recover inside of 10 yards? 20 yards? With my test method I was seeing vibrations persist from 4 to 6 seconds! That could translate into a rather large distance with the velocities we’re working with. I’ll have to see if I can figure out a way to look into that.
Now we do have lots of people reporting observations of better penetration with tapered shafts. I’m perfectly willing to accept those observations as being accurate. But I’m just not sure it’s because of superior paradox recovery. Rather, at this point I would ascribe that to the tapered shafts allowing a finer state of tune. The taper shape imposed on wood, which is inherently variable, helps each shaft more nearly behave like its mates. The initial flex created upon release occurs at more nearly identical spots on the different shafts. Its rather poor resolution but you if you look closely at the pic “Tapered Flex” you can see the flex in the arrow taking place near the beginning of the taper on that shaft.

Tapered Flex
So, if we have a bunch of woodies that all behave more nearly the same we’re also getting more consistent results during tuning. Better tune leads to a better, cleaner, launch, so paradox or not, the arrow is still travelling more nearly straight and impacts the target (animal) squarely.
It was later suggested that I look at carbon arrows. After all everybody knows that carbon recovers faster. Fine, but where’s the proof?
OK, these results will surely upset the apple cart. I went ahead and used what I could find. I also included an aluminum arrow. Using the same methods that I used with the woodies, I got the following average vibration duration times.
GT 600 Ultralight – 8.1 seconds
Easton Carbon One 780 – 9.8 seconds
Easton 1816 Platinum Plus – 11.25 seconds
These are the only explanations I can come up with for these results.
1) Since the carbons do damp faster than aluminum, and aluminum was THE shaft of choice when carbon shafts first appeared, it became accepted that carbon was better across the board, although that is not strictly true.
2) I need to test high dollar A/C/E’s and A/C/C’s. They may have lead to the belief that carbons damp faster. Being 2 dissimilar materials bonded together I would bet that they do damp out vibrations faster.
It does make sense to me in that the super regular microscopic arrangement of the carbon fibers would tend to support the creation of harmonics and standing waves rather than damp them out. This effect would be even greater in aluminum shafts with the regularity of metallic crystals down to atomic scales. Wood, with its inherent irregularities and variability would tend to damp out vibrations rather quickly, regardless of parallel or tapered.
Perhaps a cross woven carbon shaft would damp well?
Now, as a “quantifiable” measure I know that I can shoot higher scores with carbon arrows. Given that, I’m becoming more and more convinced that it is consistency that makes tapered woodies more accurate. We know how critical tuning is. So consider this, tuning is like running a specific set of experiments, If the shafts we’re tuning all behave more nearly the same the margin of error is smaller. We are able to achieve a finer state of tune. The error bars in our data acquired during tuning are smaller. Plus, once tuned, there is benefit in that the tapered all more nearly launch the same as each other as well.